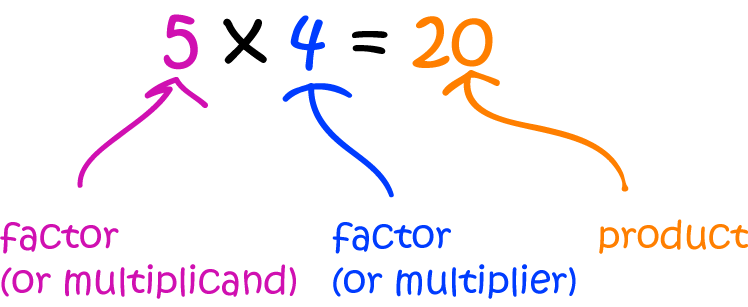Math Homework
Week 13- Nov. 12th
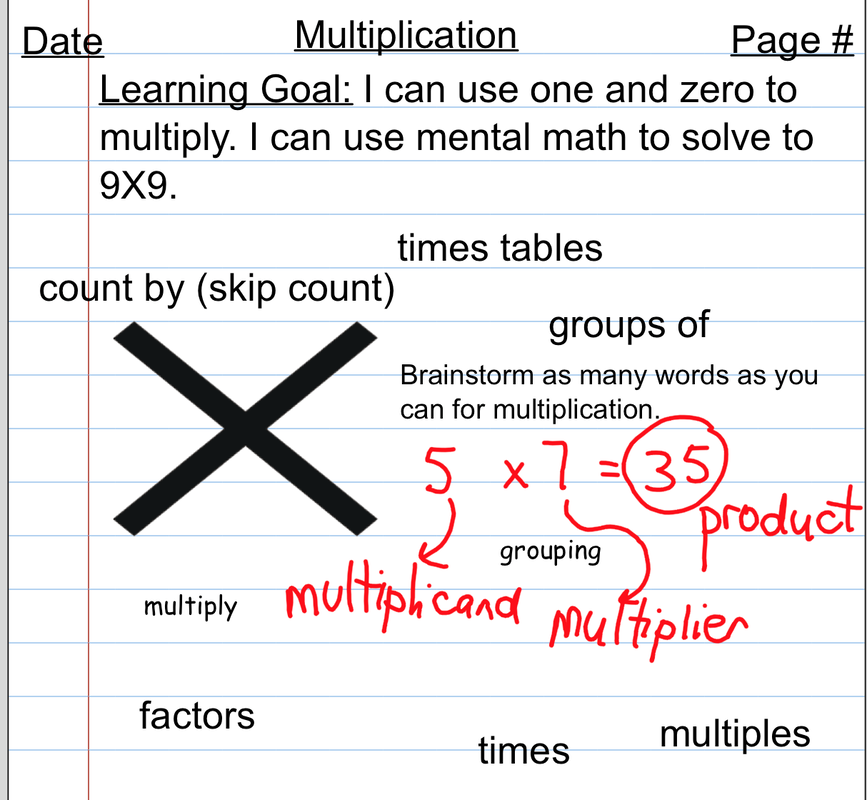
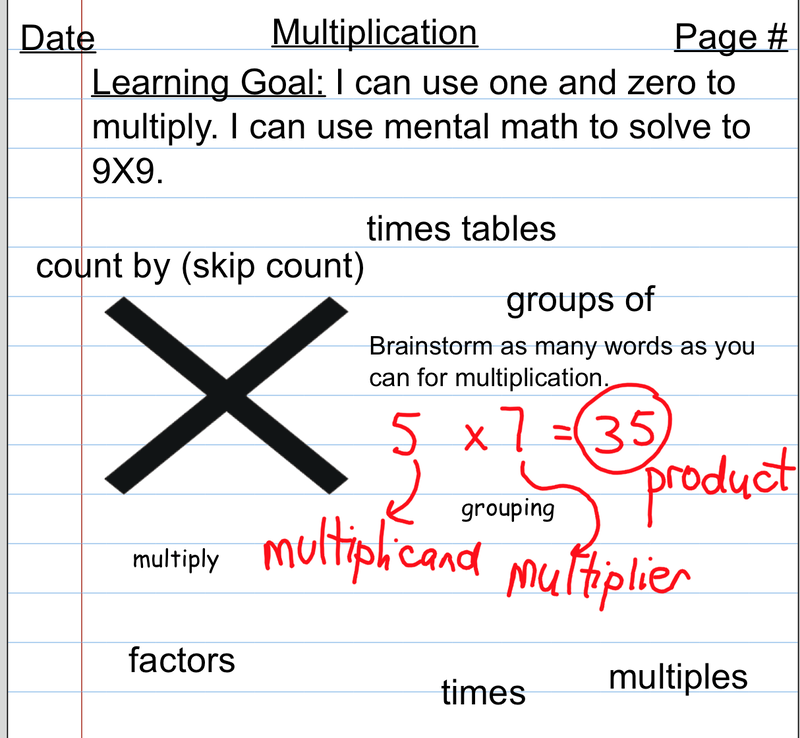
Apply the properties of 0 and 1 for multiplication and the property of 1 for division.
December Outcomes:
Read and record time, using digital and analog clocks, including 24-hour clocks.
TIME 2
Compare graphs in which the same data has been displayed using one-to-one and many-to-one correspondences, and explain how they are the same and different.
Graphing
Data Management
OCTOBER/ NOVEMBER Outcomes:
Week 13- Nov. 12th
Week 14- Nov. 18
Week 15-Nov. 25th
Week 16-Dec. 2nd
Week 17- Dec. 9th
Week 18- Jan. 6th
Week 19- Jan. 13th
Week 20-Jan. 24th
Week 21- Jan. 27th
Week 22- Feb. 3rd
Week 23- Feb.10th No Math sheet
Week 24- Feb. 18th
Week 25- Feb. 24th
Week 26- March 2
Week 27- March 9th
Week 28- March 30th
Week 17- Dec. 9th
Week 18- Jan. 6th
Week 19- Jan. 13th
Week 20-Jan. 24th
Week 21- Jan. 27th
Week 22- Feb. 3rd
Week 23- Feb.10th No Math sheet
Week 24- Feb. 18th
Week 25- Feb. 24th
Week 26- March 2
Week 27- March 9th
Week 28- March 30th
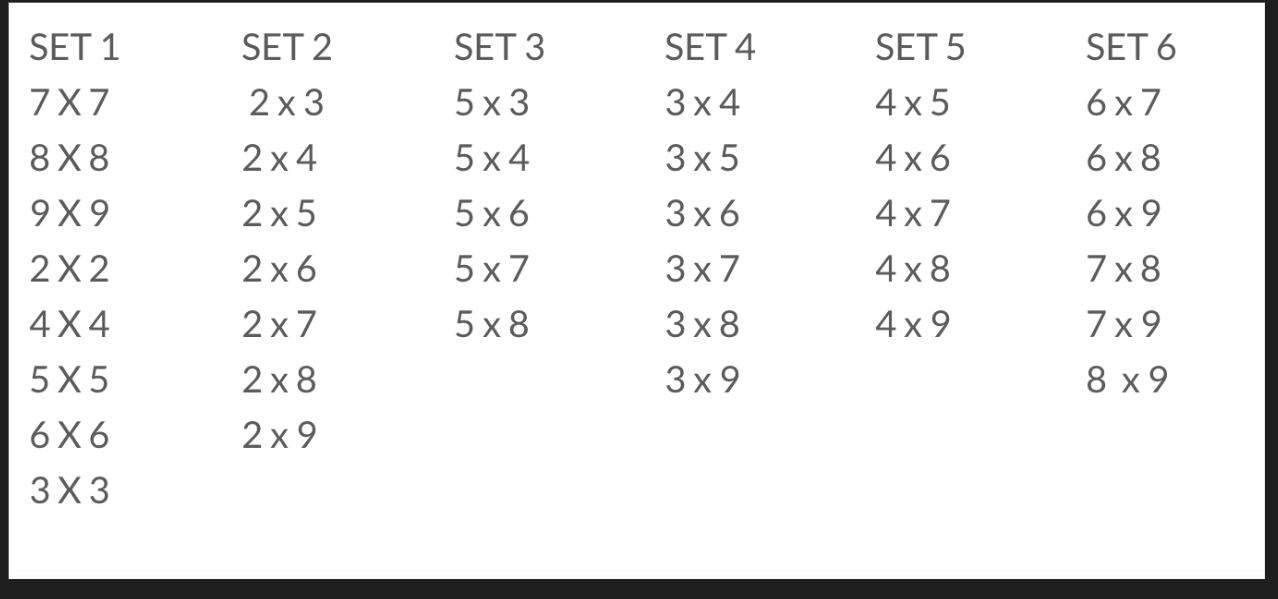
Which is why it's so frustrating to see them struggle with basic multiplication skills. Yes, many can memorize the classic 12x12 multiplication table, but give them values beyond the grid and see how fast they reach for a calculator.
Why do many students fail to grasp multiplication? Because they never gain a true conceptual understanding (beyond rote memorization) at the elementary levels.
Without deep exploration into the concept of multiplication, your kids will never truly grasp how to multiply—and this lack of understanding will surely prevent them from excelling at higher levels of math.
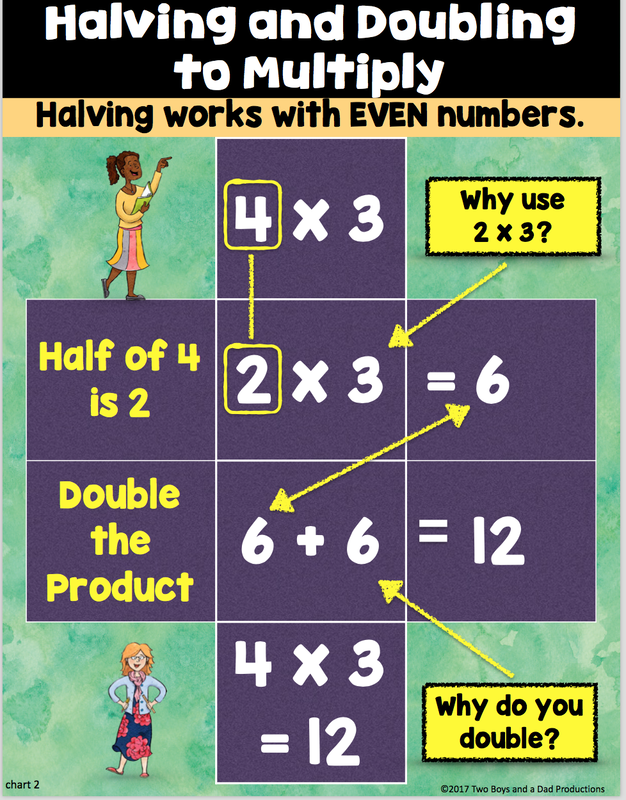
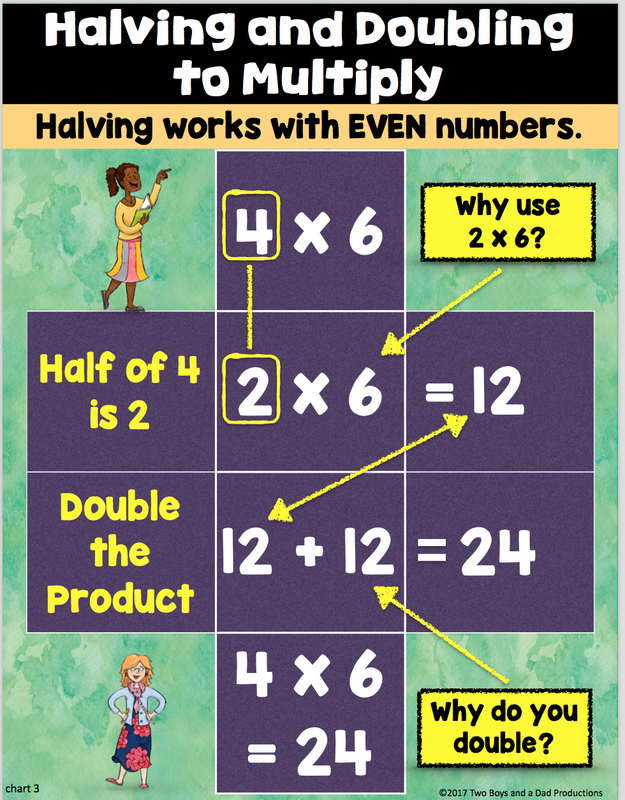
How can you help your kids to gain a deeper understanding of multiplication? Enter Area Models. And using Area Models is an awesome strategy to get kids thinking visually about multiplication, which is the approach that Mathematical Mindsets author Jo Boaler recommends most for improving math understanding.
The use of Area Models for teaching multiplication is also recommended by the National Council of Teachers of Mathematics (NCTM)!
How do they work? An area model is a visual aid that represents the product of two numbers. The model acts like a bingo board where each box represents the product ofit's corresponding row and column.
February/March 2020- Multiplication and Division
Strategies Taught in Class
Would you like to see the examples we did in class? See below attachments for the strategies taught during math.
Division Strategy #1- Long Division
This can be a little tricky because of all the steps involved. To help you with your homework, see the below files. First, you will see the SMART board lesson we did in class. Next, you will find handout given in class which outlines the steps for long division. This exact sheet will be used in class, and we'll highlight the steps in different colors to help keep you on track! Don't worry - we will spend way more time going over and over this in class!
long_division_steps_and_example.
Download File
steps_for_long_division.docx
Download File
Division Strategy #2- Base 10BlocksTo
division_strategy_1-_in_class_example.
Download File
division_strategy_1-_base_10_blocks. docx
Download File
Would you like to see the examples we did in class? See below attachments for the strategies taught during math.
Division Strategy #1- Long Division
This can be a little tricky because of all the steps involved. To help you with your homework, see the below files. First, you will see the SMART board lesson we did in class. Next, you will find handout given in class which outlines the steps for long division. This exact sheet will be used in class, and we'll highlight the steps in different colors to help keep you on track! Don't worry - we will spend way more time going over and over this in class!
long_division_steps_and_example
Download File
steps_for_long_division.docx
Download File
Division Strategy #2- Base 10
division_strategy_1-_in_class_example
Download File
division_strategy_1-_base_10_blocks
Download File
January and February 2020- Math
January- March Outcomes:Apply the properties of 0 and 1 for multiplication and the property of 1 for division.
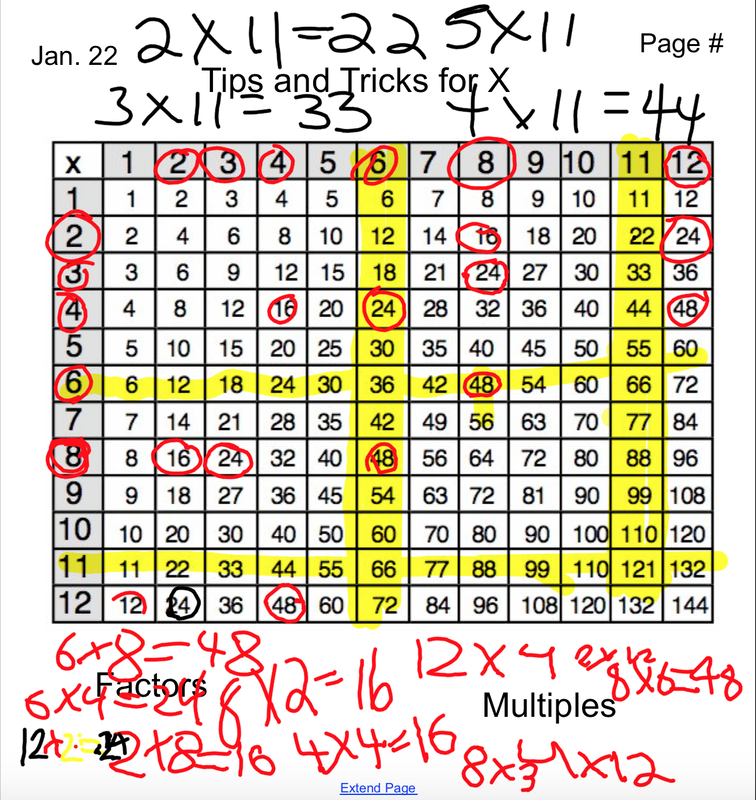
Describe and apply mental mathematics strategies such as:
skip using using patterns using
- Power Lines 1 - Mathematical reasoning level 1
- Power Lines 2 - Mathematical reasoning level 2
- Power Lines 3 - Mathematical reasoning level 3
- Sudoku Online (choose from various levels)
- Number Puzzle - Use mental math skills to solve a pyramid number puzzle.
- Sudoku Online (choose from various levels)
Demonstrate an understanding of multiplication (2- or 3-digit by 1-digit) to solve problems by
using using estimating applying
- Interactive Algebra Quiz-Distributive Property Distributive Property Worksheets
- Meteor Multiplication Arcademic Skill Builders
- Multiplication Grand Prix Multi-player
(
Demonstrate an understanding of division (1-digit divisor and up to 2-digit dividend) to solve problems by
using estimating relating
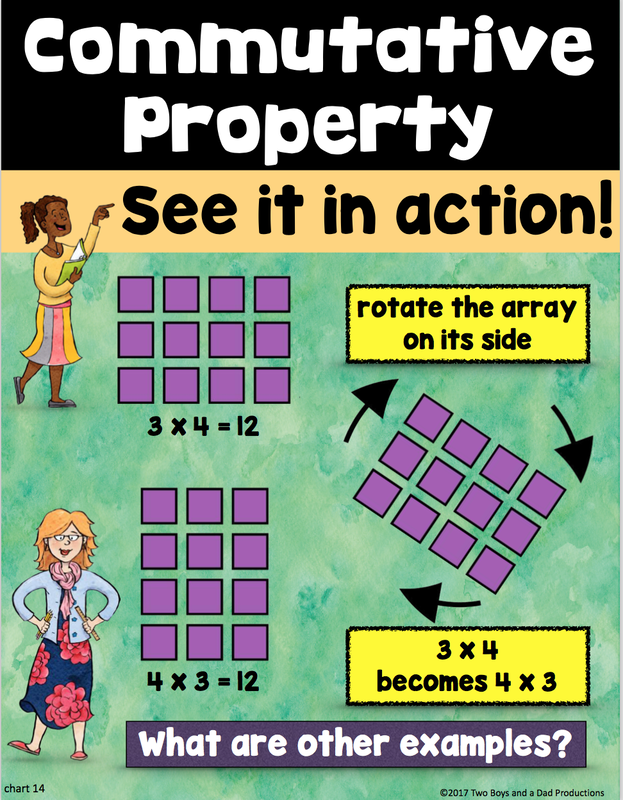
Distributive Property of Multiplication
AREA MODEL
Licence
Multiplication Properties
Distributive Property
2 and 3 digit by 1 digit multiplication
December Outcomes:
Read and record time, using digital and analog clocks, including 24-hour clocks.
- State the number of hours in a day. Express the time orally and numerically from a 12-hour analog clock.
- Express the time orally and numerically from a 24-hour analog clock. Express the time orally and numerically from a 12-hour digital clock.
- Express time orally and numerically from a 24-hour digital clock. Describe time orally as “minutes to” or “minutes after” the hour
- Explain the meaning of a.m.
and
Read and record calendar dates in a variety of formats.
- Write dates in a variety of formats; e.g., yyyy/mm/
dd dd dd - Relate dates written in the format yyyy/mm/
dd dates - Identify possible interpretations of a given date; e.g., 06/03/04.
TIME 2
Time 1
Compare graphs in which the same data has been displayed using one-to-one and many-to-one correspondences, and explain how they are the same and different.
- Find examples of graphs in print and electronic media, such as newspapers, magazines and the Internet, in which many-to-one correspondence is used; and describe the correspondence used
- Create and label (with categories, title and legend) a pictograph to display a given set of data, using many-to-one correspondence, and justify the choice of correspondence used.
- Create and label (with axes and title) a bar graph to display a given set of data, using many-to-one correspondence, and justify the choice of interval used.
- Answer a given question, using a given graph in which data is displayed using many-to-one correspondence.
- Identify an interval and correspondence for displaying a given set of data in a graph, and justify the choice.
Graphing
Data Management
OCTOBER/ NOVEMBER Outcomes:
Represent and describe whole numbers to 10 000, pictorially and symbolically.
Compare and order numbers to 10 000.
Demonstrate an understanding of addition of numbers with answers to 10 000 and their corresponding subtractions (limited to 3- and 4-digit numerals) by:
Add and Subtract
Symmetry
Estimation
Compensation Strategy is the same as Front-End Estimation, only you are 'compensating' for the amount
468 + 298 =
400 + 200 = 600 + 100 = 700
For the month of September we focused on Growth Mindset in Math, including how to work through a problem without giving up. We worked through several challenges using YOUCUBED, and their week of Inspirational Math. Students learned how math is used in everyday life and how to 'play' with math in order to learn how to have fun with math problems.
Students also learned how to multiply and divide by 10 to find the pattern in place value.
Compare and order numbers to 10 000.
Demonstrate an understanding of addition of numbers with answers to 10 000 and their corresponding subtractions (limited to 3- and 4-digit numerals) by:
• using
• estimating
• solving
Represent and describe decimals (tenths and hundredths), concretely, pictorially
and symbolically.
Identify and describe patterns found in tables and charts.
Demonstrate an understanding of line symmetry by
Construct and interpret pictographs and bar graphs involving many-to-one correspondence to draw conclusions.
Demonstrate an understanding of many-to-one correspondence.
Students are completing a data collection project for Waste in Our World in order to organize and analyze the results. We will be using their data to create and interpret graphs of their results. See Science for the project details.
Construct and interpret pictographs and bar graphs involving many-to-one correspondence to draw conclusions.
Demonstrate an understanding of many-to-one correspondence.
Students are completing a data collection project for Waste in Our World in order to organize and analyze the results. We will be using their data to create and interpret graphs of their results. See Science for the project details.
Click on the below concept to learn more:
DecimalsAdd and Subtract
Symmetry
Estimation
Estimate sums and differences, using different strategies; e.g., front-end estimation and compensation.
468 + 298 =
400 + 200 = 600 + 100 = 700
Students also learned how to multiply and divide by 10 to find the pattern in place value.
Math in the Workforce

Number Fact Fluency
Communicating with Parents
What is number fact fluency?
Number fact fluency refers to a student’s ability to think efficiently, accurately and flexibly towards mastery using numbers. A number fact is defined as addition and subtraction expressions up to 20 and multiplication and division expressions up to 100.
Why do we focus on number fact fluency?
Students with strong number sense are able to manipulate numbers and understand how to use various strategies to solve problems. Students develop their number fluency along a continuum of learning that starts with basic counting skills that leads to efficient strategies that may include recall. Recall is the ability to effortlessly know the answer as a result of developing strategies and number relationships (Lawson, 2016).
How do teachers assess number fact fluency?
It is important to gather a body of evidence about each student’s number fact fluency. A balanced body of evidence includes observations ofprocess
Observations of students playing games or participating in number talks Math Running Records Assessment
Computation student work samples
Communicating number fact fluency with parents
Each student’s progress in mathematics learning needs to be evident to them, their teachers and their families. In order to communicate a students number fact fluency a document has been created called “My Child’s Path to Number Fact Fluency” which outlines the learning progression that students move through as they develop mastery using numbers. Once a teacher has gathered a body of evidence they can then indicate the student’s current understanding using the arrow. The intention of this document is to help parents understand their child’s learning as well as next steps in order to move them along the continuum.
What is number fact fluency?
Number fact fluency refers to a student’s ability to think efficiently, accurately and flexibly towards mastery using numbers. A number fact is defined as addition and subtraction expressions up to 20 and multiplication and division expressions up to 100.
Why do we focus on number fact fluency?
Students with strong number sense are able to manipulate numbers and understand how to use various strategies to solve problems. Students develop their number fluency along a continuum of learning that starts with basic counting skills that leads to efficient strategies that may include recall. Recall is the ability to effortlessly know the answer as a result of developing strategies and number relationships (Lawson, 2016).
How do teachers assess number fact fluency?
It is important to gather a body of evidence about each student’s number fact fluency. A balanced body of evidence includes observations of
Observations of students playing games or participating in number talks Math Running Records Assessment
Computation student work samples
Communicating number fact fluency with parents
Each student’s progress in mathematics learning needs to be evident to them, their teachers and their families. In order to communicate a students number fact fluency a document has been created called “My Child’s Path to Number Fact Fluency” which outlines the learning progression that students move through as they develop mastery using numbers. Once a teacher has gathered a body of evidence they can then indicate the student’s current understanding using the arrow. The intention of this document is to help parents understand their child’s learning as well as next steps in order to move them along the continuum.